Paper: A mechanistic model of spherical particle entrapment in elliptical contacts.
Author: George K. Nikas
Published
in: Proceedings of the
Institution of Mechanical Engineers, Part J: Journal of Engineering
Tribology, 2006, 220(6), 507-522
Errata: In Eqs. (25), second equation from the top (case x > xin), h should be changed to h2.This is only a misprint. Moreover, in Fig. 5, the labels of the vertical axis must be divided by 10. Accordingly, the peak value quoted in the text on page 516 (left column) must be 0.5 N instead of 5 N.
Abstract
The dynamic interaction of solid, spherical particles with the counterfaces of concentrated, dry or lubricated, conforming or nonconforming, rolling-sliding elliptical contacts is mathematically analysed. Criteria for the entrapment or rejection of particles are postulated, based on the resolution of mechanical and fluid forces on a particle for given contact geometry and operating conditions. Three-dimensional maps of the various force components on a particle are presented for a typical application, together with maps of the zones where a particle would be “conditionally” entrapped, “weakly” rejected or “unconditionally” rejected, where the previous terms are defined in a comprehensive evaluation system in the model to assess the risk of damage of the contact from the presence of contaminants. This study is concerned with the process of particle entrapment, meaning that a particle must be in contact with both counterfaces of a concentrated contact, and not entrainment (particle wandering in the lubricant, which has been studied by the author in [reference]). To the best of the author’s knowledge, this is the first study explicitly dealing with the general case of elliptical contacts. Elliptical contacts cover both circular contacts and, taken to the limit, can also simulate line contacts; thus, the model’s applicability and validity as a design tool is generalized. In summary, the purpose of the paper is to expand previous models developed for simpler geometries and to present an effective computational tool for the simulation of particle entry into elliptical contacts and the resulting risks of contact damage.
Some figures from this work
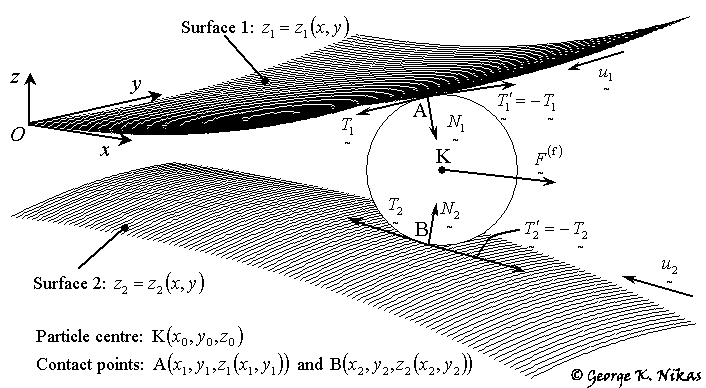
Figure 1 shows a spherical particle of centre K in contact with the counterfaces (surfaces 1 and 2) of an elliptical contact at points A and B. After calculating the geometry of the contact during operation, that is, functions z1(x, y) and z2(x, y) as in Fig. 1, then, given the coordinates (x0, y0) of the particle’s centre K, contact points A and B are geometrically located, and the particle diameter and z-coordinate of K (z0) are calculated.

Fig. 1. Contact surfaces and particle forces.
This is followed by a mechanical force analysis on the particle, involving the normal contact forces N1 and N2 (see Fig. 1), the frictional forces T1 (or -T1) and T2 (or -T2), and the resultant fluid force on the particle, F(f). Force equilibrium dictates the resultant force on the particle and the direction of that resultant force dictates the probability of entrapment or rejection of the particle at the given position, based on special criteria that are comprehensively developed in the article. The process is repeated for hundreds of positions (x0, y0).
An example of the x-component of the resultant force on a particle (force Fx) is shown in Fig. 2. What Fig. 2 shows is a distribution of force Fx in the solution domain, which is an area of size 16Dx ´ 20Dy at the inlet zone of the contact (taking advantage of symmetry about the y = 0 plane), Dx and Dy being the lengths of the contact ellipse semi-axes. Figure 2 shows not only the magnitude of force Fx and how this varies in the solution domain, but also the zones of particle "entrapment" (x/Dx < 3 in this example), "weak rejection" (3 < x/Dx < 12) and "unconditional rejection" (x/Dx > 12), which is the result of the entrapment analysis or evaluation based on the previously mentioned special criteria.
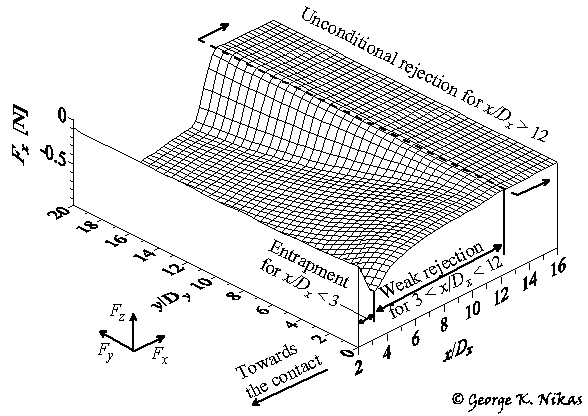
Fig. 2. Example of the x-component (Fx) of the particle resultant force.
The terms "entrapment", "weak rejection", "unconditional rejection", as well as "rejection", "potential rejection" and "conditional entrapment" are defined in the article and are used to deal with the uncertainties involved, which are owed to the assumptions of the model, that is, that particles are spherical and rigid. Figures similar to Fig. 2 are presented in the article for other mechanical and fluid force components.
Based on the force and entrapment analysis, maps of the particle entrapment risk in the elliptical contact are constructed for visualisation of the risk zones. Such a map is shown in Fig. 3.
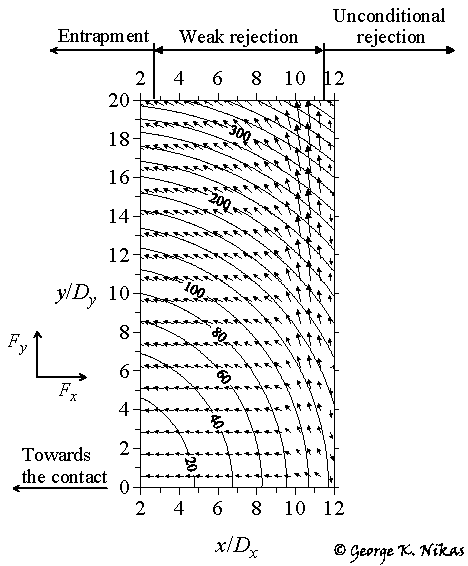
Fig. 3. Force vector (Fx, Fy) (shown with distributed arrows) and contour map of particle diameters with labels 20, 40 … 300 for particle diameter in micrometres.
The elegance of this presentation lies in the fact that the cause as well as the "strength" of particle entrapment or rejection are both realised by looking at the angle and length of the force arrows in Fig. 3.
Among other useful results in the article is the effect of the friction coefficients of the counterfaces on particle rejection, which is useful not only for assessing the risk of damage from debris particles but also for evaluating the effect of surface coatings in protecting the contact from potentially harmful contaminants by preventing their entry in the first place.