Paper: Debris particle indentation and abrasion of machine element contacts: an experimentally validated, thermoelastoplastic numerical model with micro-hardness and frictional heating effects.
Author: George K. Nikas
Published
in: Proceedings of the Institution of Mechanical Engineers
(IMechE), Part J: Journal of Engineering Tribology, 2013, 227(6),
579-617
Abstract
For a very long time, debris particles have been blamed to causing serious problems in machine-element contacts such as those of bearings and gears. This involves a huge number of mechanisms and machines worldwide. The financial cost associated with machinery failure under such circumstances is enormous. Past research has identified the main mechanisms governing damage from debris particles. A few theoretical models have been built on the experience accumulated on damage mechanics. The capabilities of said models vary a lot. The model originally developed by this author in the 1990s was recently expanded. The previous version of the model, which was published in this journal in May 2012, offered a number of innovative features to calculate spherical-particle indentation and soft abrasion in lubricated rolling-sliding contacts. It was experimentally validated following a rigorous programme. However, it neglected frictional heating from particle extrusion. This study significantly expands the previous model of the author by integrating thermal effects. It includes flash temperature calculations with moving sources of heat, dynamic heat partition, 3D conduction and convection, and thermally anisotropic surfaces with temperature-dependent thermal and mechanical properties, all integrated in the elastoplastic model of indentation and abrasion. These are in addition to model features such as nonlinear strain hardening, strain-gradient plasticity, particle work hardening, generalised local kinematics, pile-up/sink-in plasticity effects and many more. The same rigorous experimental verification programme as in the previous model of the author is used here, too. It is shown that in some cases, the theoretical results on dent geometry are even closer to the experimental ones than with the isothermal model of the author. Furthermore, the thermal analysis reveals that extreme frictional heating can take place, often leading to melting wear in a fraction of a millisecond. The formation of dimples inside and outside main dents, which have been shown experimentally and verified theoretically by this author’s previous model, is revisited in light of frictional heating. A parametric study shows the effects of particle size and hardness, kinetic friction coefficients, and strain hardening on dent geometry and flash temperatures, including effects on particle and surface melting. Finally, the reality of flash temperatures is explored.
Some figures from this work
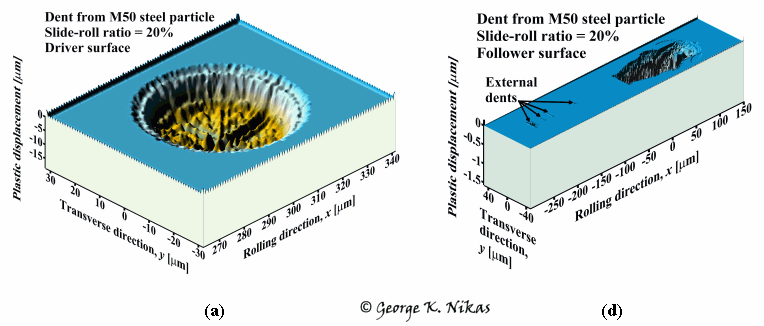
Figure 1 shows one of several examples numerically analysed in the paper, namely the dents generated by a spherical M50 steel particle trapped in an elastohydrodynamic, rolling-sliding contact of rotating spherical discs made of AISI 52100 steel. This is based on a real case analysed in an experimental study by Ville and Nelias. Particle and disc hardnesses are almost equal (750 Vickers). The slide-roll ratio between the discs is 20% in this case. Figure 1 shows not only the geometry of the dents and their precise dimensions, which are in accord with the experimental results of Ville and Nelias. The simulation confirms the existence of external dents and bottom holes or dimples inside dents as depicted in figure 1, in agreement with experimental data.



Fig. 1. Numerical simulation of the indentation of elastohydrodynamically lubricated, rolling-sliding, bearing-steel surfaces by a 36 micron, M50 steel particle for 20% slide-roll ratio (this is based on a real case published in an experimental study of Ville and Nelias). Graphs (a) to (c) are for the driver surface; graphs (d) to (f) are for the follower surface.
Figure 2 demonstrates the numerically analysed process of indentation and dimple formation for input data taken from a real case of a rolling elastohydrodynamic contact. Elastohydrodynamic gap thickness, particle force and pressure, and dent depth are all depicted in figure 2. The whole incident takes place in just 6 hundredths of a millisecond (0.06 ms). As the particle is severely sheared, compressed and extruded, frictional heating at its interfaces with the elastohydrodynamic contact counterfaces as well as frictional heat generated inside the plastically deforming particle is so intense that flash temperatures up to the melting point of the contact counterfaces (1450 °C) are rapidly reached, as depicted in figure 2. Localised surface melting is clearly predicted in this case.
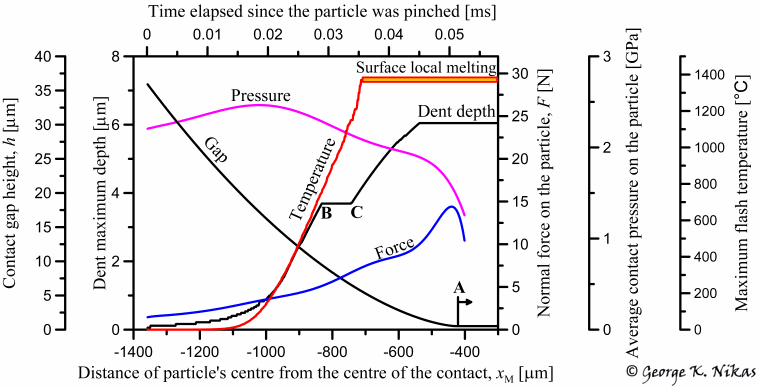
Fig. 2. The dynamic process of indentation by a 36 micron M50 steel particle in a rolling elastohydrodynamic contact of steel spherical discs, based on the experimental results of Ville and Nelias. Dimple formation potentially takes place before point B (from left to right). "Gap" refers to the elastohydrodynamic contact gap; "pressure" and "force" refer to those exerted to the particle during its compression in the contact. Finally, point A signifies the entrance to the Hertzian zone of the contact.
Several examples concerning various particles are analysed in the paper, including copper particles (90 Vickers), low-carbon steel particles (150 Vickers), and high-carbon steel particles (750 Vickers) in rolling and rolling-sliding contacts. Input data for all cases are adapted from the experimental literature and the numerical results are thoroughly compared with those derived experimentally.
The paper continues with a parametric study of the effects of particle size, particle initial hardness, strain-hardening properties and friction on the dimensions of dents (surfacial dimensions, depth, volume and average slope), as well as on particle and surface flash temperatures from frictional heating. An example of the parametric study is shown in figure 3.
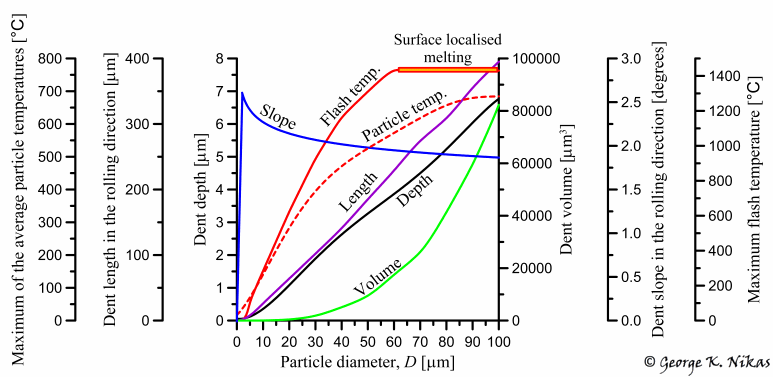
Fig. 3. Example of the parametric study of the paper concerning a rolling elastohydrodynamic contact (steel surfaces of 700 Vickers hardness) disturbed by a spherical steel particle of 200 Vickers hardness. Numerical analysis of the effect of particle size on dent dimensions, volume and slope in the rolling direction, particle temperature and maximum flash temperature in the contact. It is clear that for large particles (60 micron and over in this case), flash temperatures reach the melting point of the material of the surfaces in the contact.