Paper: Effects of operating conditions and friction on the entrapment of spherical debris particles in elliptical contacts.
Authors: George K. Nikas
Published
in: Proceedings of the
Institution of Mechanical Engineers, Part J: Journal of Engineering
Tribology, 2007, 221(6), 727-741
Abstract
Based on a mechanistic model of entrapment and rejection of spherical debris particles in elliptical contacts of various machine elements, which has been recently published by the present author, a parametric study has been conducted to analyse the effects of the contact load and speed, lubricant viscosity (in the case of lubricated contacts) and particle-contact-counterface friction coefficients on the critical particle size for entrapment, rejection and intermediate states. The simulation involved a conforming as well as a non-conforming elliptical contact. The parameters were varied in unequal steps as follows: the contact load from 5 to 500 N, the contact speed (average speed of the two counterfaces) from 0.005 to 5.500 m/s, the lubricant dynamic viscosity from 0.001 to 1.000 Pa·s, and the friction coefficient between a particle and a contact counterface from 0.02 to 0.20 (with, generally, different coefficients used for the two counterfaces). The results are in the form of two- and three- dimensional graphs and contour maps, showing the zones of particle entrapment, rejection, “weak rejection”, etc, in the contact inlet, the critical particle sizes for entrapment and rejection, as well as graphs showing most of these parameters and effects together for quick assessment. The model has proved an efficient mathematical tool in predicting the risks of contact damage from debris particles by offering both clear quantitative as well as qualitative answers, and can assist in the selection of proper filtration or sealing systems, or simply be used as a supplementary tool in life-expectancy calculations of concentrated contacts in machine-element applications.
Some figures from this work
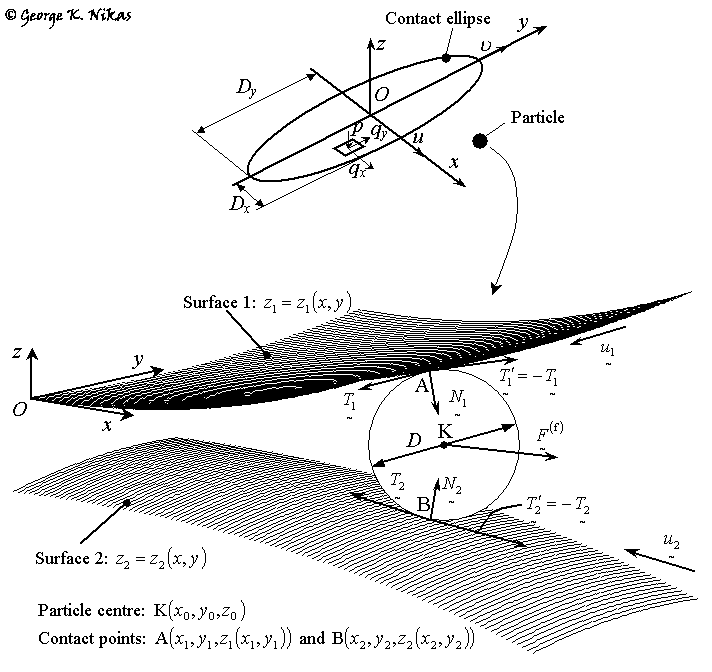
Figure 1 shows a spherical particle of centre K in contact with the counterfaces (surfaces 1 and 2) of an elliptical contact at points A and B.

Fig. 1. Debris particle contacting the counterfaces of an elliptical contact.
The calculation of the contact geometry, the location of particle contact points A and B, the calculation of the particle-counterface normal and frictional contact forces, as well as the calculation of the fluid force on the particle from the lubricant used in the contact, are all described in a previous publication of the author and briefly summarized in the present paper. Based on the force resolution on the particle, suitable criteria for entrapment, "unconditional rejection", "weak rejection", etc, are applied, as postulated in the related previous publication of the author and summarized in the present paper.
Figure 2 shows one of the many maps presented in the paper, depicting part of the contact inlet, where x is along the line of motion and point (x = 0, y = 0) is the contact centre.
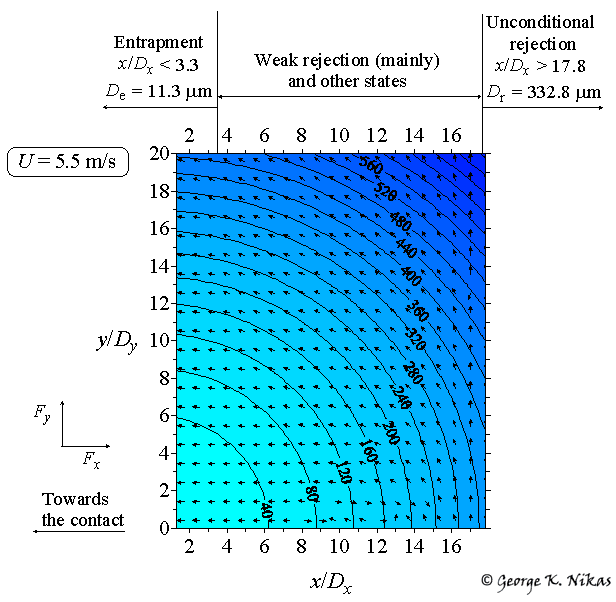
Fig. 2. Force vectors (Fx, Fy) (shown with distributed arrows) and contour map of particle diameters with labels 40, 80…560 for particle diameter in micrometres.
The map shows the fluid film contour lines (the labels are in micrometres). A spherical particle in geometrical contact with both counterfaces at a position (x, y) has diameter approximately equal to the film thickness at that position, thus the contour lines also depict the particle diameter for a particle to be in geometrical (that is undeformed) contact with the counterfaces. The map also shows the projection on the xy-plane (tangent plane of the elliptical contact) of the total force on particles in contact with the counterfaces by means of distributed arrows. Looking at the angles of the arrows, it is easy to establish where a particle is dragged towards the contact and where it is pushed away. Also on the map, the zones of particle entrapment, unconditional rejection, weak rejection, etc, are clearly shown and quantitatively defined. For the example shown in Fig. 2, the maximum particle diameter for entrapment at the centreline of the contact (y = 0), De, and the minimum particle diameter for unconditional rejection, Dr, are calculated equal to 11.3 and 332.8 microns, respectively. Maps like that are presented in the paper for various lubricant viscosities, contact loads and speeds.
Another form of mapping discussed in the paper concerns the effect of the Coulomb friction coefficients, m1 and m2, between a particle and the contact counterfaces. Figure 3 shows such an example for a conforming contact, where it is clear that the effect of the friction coefficients on the minimum particle diameter for unconditional rejection, Dr, is significant. Figure 3 shows both a surface and the corresponding contour map overlaid for best visualization.
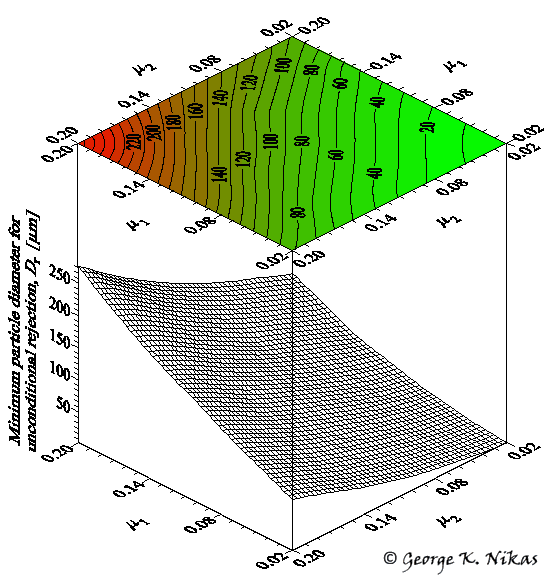
Fig. 3. Example of the effect of the counterface friction coefficients.
The paper ultimately presents figures showing the effects of contact load, contact speed, and lubricant dynamic viscosity on the critical particle diameters for entrapment and unconditional rejection, following a parametric study. Such results are presented in Fig. 4 for a conforming elliptical contact.
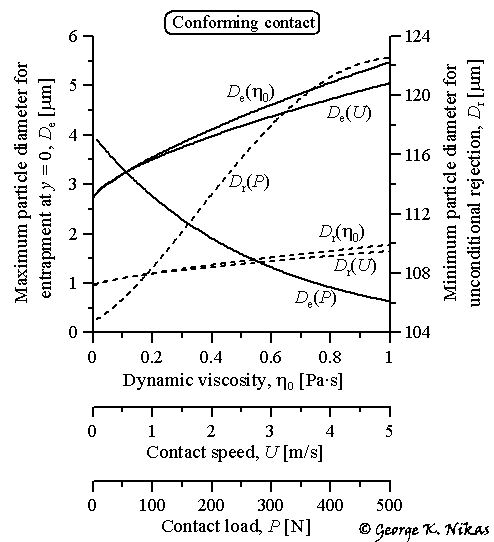
Fig. 4. Effects of the lubricant dynamic viscosity, contact speed and load.
It is thus easy to quickly evaluate the risks involved in a particular elliptical contact under specific operating conditions in terms of debris particle contamination...