Paper: Algebraic equations for the pile-up geometry in debris particle indentation of rolling elastohydrodynamic contacts.
Author: George K. Nikas
Published
in: Transactions of the American Society of Mechanical
Engineers (ASME), Journal of Tribology, 2016, 138(2),
021503-14
Metallic micro-particles of 5 to 100 micrometers in size often contaminate elastohydrodynamic (EHD) contacts and indent surfaces. The geometrical characteristics of dents by such solid particles are linked to the way surface damage may evolve and how it may affect the life of the damaged contacts. In many cases, debris dents appear with shoulders raised above the original surface. Material piling-up this way causes high pressure spikes when dents are overrolled by an element such as a ball in a rolling bearing. This study introduces an approximate analytical method based on the so-called expanding cavity model to calculate pile-up geometry with simple algebraic equations in thermoviscoplastic indentation of rolling EHD contacts by ductile spherical micro-particles. Based on an experimentally validated debris indentation model published by the author, the pile-up model is shown to give realistic predictions in a wide range of operating parameters. Upon experimental validation, the new model is used to study the effects of particle size and hardness, Coulomb friction coefficient, strain hardening and rolling velocity of EHD contacts on pile-up geometrical parameters including length, height, volume and curvature.
Some figures and details from this work
An expanding cavity model (ECM) incorporating strain-hardening and indentation-size effects is at the core of the author's indentation model. The formulation of the ECM for spherical indentation is shown in Fig. 1.

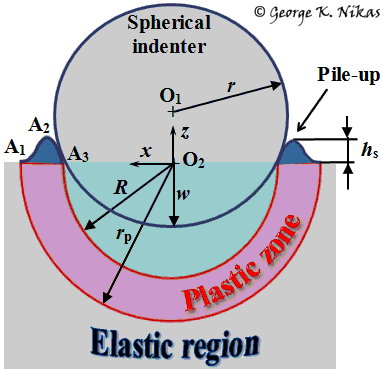
Fig. 1. Pile-up geometry of the indentation model (not to scale).
A rigid spherical indenter (O1, r) penetrates an elastic half-space to a depth w. Above a certain elastic limit, the penetration is elastoplastic. The contact interface of the indenter and the half-space is contained in a hemispherical hydrostatic core (O2, R). In turn, the core is enclosed by an incompressible plastic zone of inner radius R and outer radius rp. Further outward lies the region where all displacements are elastic. At the unrestricted surface of the plastic zone, material is free to pile-up if contact conditions are favourable. In other words, compressed material can permanently budge above the original surface at the free boundary of the plastic zone. Thus, pile-up such as A1A2A3A1 in Fig.1 is formed.
An analytical model is founded on the ECM concept of Fig. 1. Through a geometrical analysis and in conjunction with the author's experimentally validated thermoviscoplastic indentation model [1, 2, 3, 4] for debris particles in elastohydrodynamic contacts, a system of algebraic equations has been developed to calculate the pile-up geometry when disc-shaped ductile particles are dynamically extruded in rolling elastohydrodynamic (EHD) contacts. After experimental validation, the pile-up model is used to study the effects of particle size and hardness, Coulomb friction coefficient, strain hardening and rolling velocity of EHD contacts on pile-up geometrical parameters including length, height, volume and radius of curvature.
Figure 2 shows an example of the parametric study. It concerns the effect of the strain-hardening exponent of the indented solid on the pile-up geometrical parameters, namely length (L = rp – R), height (hs), volume (Vpu) and radius of curvature (rho). The maximum surface temperature (theta_max) from the frictional heat generated during the indentation process is also depicted in Fig. 2. This example is for a 20 micrometer spherical particle with cold hardness of 700 HV, indenting a 700 HV steel surface in a line EHD contact rolling at 1 m/s.

Fig. 2. Effect of the strain-hardening exponent of the indented solid on geometrical parameters of the pile-up.
The benefit of results such as those in Fig. 2 is in assessing the evolution of surface damage when debris-induced dents are overroled as in the case of a rolling bearing. Dent shoulders (pile-up) act as dynamic stress raisers when overrolled by a rolling element such as a ball in a rolling bearing, even in the presence of a thick lubricating film. The result could be accelerated wear in the form of spalling.