Paper: Particle extrusion in elastohydrodynamic line contacts: dynamic forces and energy consumption.
Author: George K. Nikas
Published
in: Proceedings of the Institution of Mechanical Engineers
(IMechE), Part J: Journal of Engineering Tribology, 2017, 231(10),
1320-1340
The authorís model of particle entrapment and thermoviscoplastic indentation built and experimentally validated in recent publications is utilised to calculate the contact forces on ductile, isolated interference particles passing through elastohydrodynamic, rolling-sliding, line contacts. The model is detailed and enriched by supplementary equations. A parametric study deals with the effects of particle size and cold hardness, kinetic friction coefficient, rolling velocity and slide-roll ratio of the contact on the particle contact forces, mean friction coefficient, temperature, plastic work and power required to deform a particle, as well as on dent volume and plastic strain rates of the indented contact surfaces. A factual selection of optimal conditions and parameter values that minimise the disruption of a contaminated contact is thus greatly facilitated.
Some figures and details from this work
The author's model on the thermoviscoplastic indentation of concentrated line contacts by ductile micro-particles has been built in stages and experimentally validated in various published articles [1, 2, 3, 4, 5]. It normally deals with metallic particles of at least 1 micrometre in spherical diameter, trapped and passing through rolling-sliding, dry or lubricated contacts. The model accounts for a large number of parameters, including geometrical, kinematical, material and dynamic parameters. In the present article, the model is enhanced by supplementary equations to calculate the dynamic contact forces during the passage of a particle through elastohydrodynamic line contacts. Additionally, the mean friction coefficient between the particle and the contact counter-surfaces is computed along the path of the particle. Finally, the plastic work and power required to deform the particle are also calculated. The dynamic calculations involve the thermoviscoplasticity of the deforming solids in the process, that is, the effect of the plastic strain rates and temperature on surface deflections and particle deformation, which are dynamically varied by frictional heating among others factors.
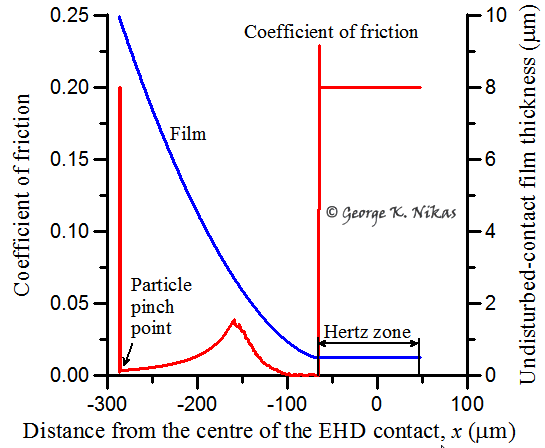
Figure 1 shows an example of the mean friction coefficient at the interface between a 10 micrometre steel particle passing through a rolling, line, elastohydrodynamic contact of central film thickness equal to 0.5 micrometres. The journey of the particle lasts only 0.33 milliseconds.

Fig. 1. Mean coefficient of friction between a 10 micrometre spherical particle and the contact counterfaces as the particle passes through a rolling, line, elastohydrodynamic contact in just 0.33 milliseconds.
The kinematic coefficient of friction in this example equals 0.2. However, it is seen in Fig. 1 that the latter actually holds only at the beginning and during the ending of the particle's journey. As soon as the particle is pinched, the effective coefficient of friction (the ratio of the average friction force on the deforming particle over the normal force) is substantially decreased. This is so because the particle is extruded, that is, it collapses almost axisymmetrically in a way that the resultant friction force on its collapsing faces is very low (local tractions on its faces are still high but are anti-diametrically self-cancelled to a great extent). Eventually, there is some asymmetry in the way a dent is formed and, consequently, on the traction distribution on the faces of the collapsing particle, which is evident in Fig. 1 by the rising and falling coefficient of friction. When the particle crosses the entrance of the flat Hertzian zone of the contact, said asymmetry is maximized with a characteristic peak in the coefficient of friction. Corresponding peaks exist for the normal and the frictional force and can be corresponded to a simultaneous distinctive knock or acoustic emission. These results prove that a simplistic analysis with a constant coefficient of friction as in some other studies is clearly inefficient, even as an approximation.
In a parametric analysis in the article, the effects of particle size and cold hardness, kinetic friction coefficient, rolling velocity and slide-roll ratio of the contact on the particle contact forces, mean coefficient of friction, temperature, plastic work and power required to deform a particle, as well as on dent volume and plastic strain rates of the indented contact surfaces are examined in 14 figures with a total 62 performance curves. An example from the parametric study is shown in Fig. 2.
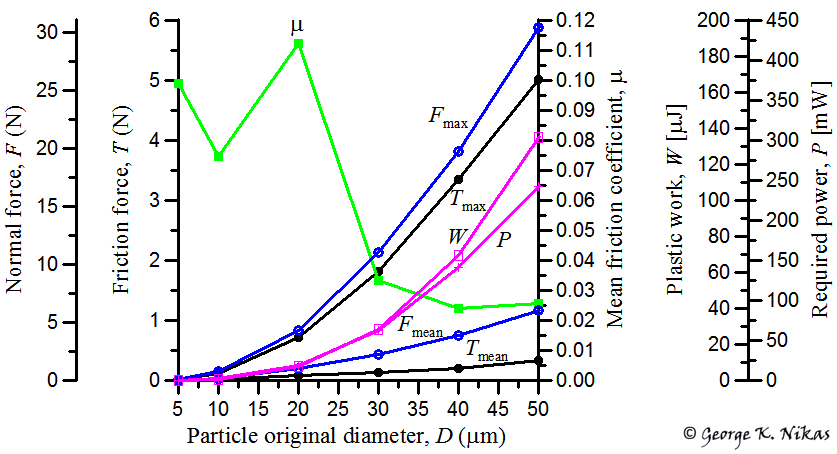
Fig. 2. Effect of the original particle diameter (example from the parametric analysis in the article). The time for a particle to pass through this elastohydrodynamic line contact of 0.49 micrometre central film thickness varies from 0.27 ms for the 5 micrometre particle to 0.56 ms for the 50 micrometre particle. "max" and "mean" refer to maximum and mean value, respectively.
Figure 2 shows the effect of the diameter of the originally spherical particle on the particle normal and frictional force, mean coefficient of friction between the particle and the contact counter-surfaces, plastic work to deform the particle and required power to do so. Results like these are assessed in the article in relation to plastic strain rates, flash temperatures from frictional heating and dynamic dent volumes during the particle extrusion and progressive indentation. Critical parameters are thus established and conclusions are reached as to how damage can be minimized.